“選區劃分與統計物理”專題研究計畫
(Taming the
Gerrymander
--Statistical Physics Approach to
Political Districting Problem)
本網頁編寫人：鄒忠毅。
最後修改時間：
摘要：
因應我國2005年修憲後，立法委員選舉採單一選區兩票制的新制度的實際需要。我們想到了將統計物理方法應用在選區劃分問題上，也做了一些嘗試。
以下我們將介紹，選區劃分問題與
q-state Potts 模型的對應關係。及以台北市為實例，介紹我們如何把真實世界資料變成可解物理模型的工作流程，及如何用遺傳算法與模擬退火法來實際求解。我們也將報告兩種方法的計算結果比較，及一些在不同參數下所得的台北市立法委員選區劃分的結果。依照中選會初步決定的劃分原則，“縣市內每一選區的人口數相差不得超過百分之十五”。而我們所得的劃分結果，人口數相差約可達到百分之一，遠好於中選會的標準。
此外，我們也正在研究這套模型與方法的拓展性，希望能將它應用在更廣泛的區域劃分問題上。
參與成員：
一，老師：
中國文化大學政治研究所：楊泰順教授
二，學生：
中國文化大學物理系：朱祐苓，曾建誌，涂悅琪，方彥理，余仁傑，李彥慧，邵天嬋。
中國文化大學政治研究所：陳彥祐，趙志勳
緣起：
在2005年我國憲法增修過程完成後，立法委員選舉將改為單一選區兩票制。可以預見的是，這個新制度的實施，將對社會產生種種衝擊。其中最大的問題，就是如何劃分選區（圖一）。我們聯想到，也許可以將統計物理方法應用到選區劃分問題上。所以就做了一些初步的研究[1]。
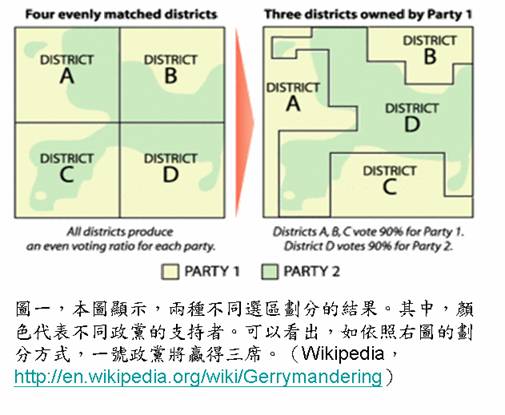
問題：
選區劃分問題是指，如何將一個較大的行政區域（如縣或市）依照一定規則，劃分為數個選舉區。在一般政治學研究裡[2] ，廣義的選區劃分有人與以地為主的兩種分別。但我們在這裡所討論的選區劃分問題是指，如何將一個較大的行政區域（如縣或市）依照一定規則，劃分為數個小選舉區。
又在政治學的研究中，選區劃分並沒有一個固定原則可循，不同的歷史背景、社會結構及政治生態均會引響劃分的結果，所以各國均有不同的劃分原則。但一般來說，選區劃分依然有些規則要遵循。例如，各選區的選民數應該相近，以符合票票等值的原則。又選區的界線應該簡潔而連續，以並免歷史上傑利蠑螈的故事重演
(圖二)，且較能避免爭議。
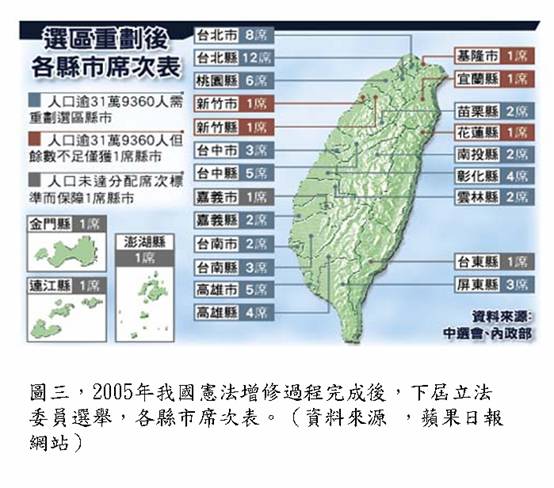
以下介紹我國下屆立委選舉的規劃。因應下屆立法委員選舉（圖三），我國中央選舉委員會，也初步訂立了一些劃分原則來保障“票票等值”及“行政區域完整”等基本精神。其中最重要的原則是，“縣市內每一選區人口數相差不得超過百分之十五 ”（圖四）。目前實際的劃分作業，仍在各縣市規劃進行中。但可以預見，由於選區劃分直接與地方政治生態有關，未來各選區實際劃分的過程，一定會受到社會大眾的關注。所以我們覺得，如果有一個可以量化的系統性的方法，是可以減少很多爭議的。
物理模型：
我們嘗試把政治學上的選區劃分問題映射到 q-state Potts 模型[3]上。在這個模型裡，
我們以“里”這個最小行政單位為模型中的自旋子單元，而種種選區劃分時的主要考慮，也被轉換為每個自旋子間的交互作用與外場對系統的作用。而選區劃分問題也就成為尋找這個 q-state Potts 模型系統的基態問題。
首先報告如何建立模型。我們定義自旋子（里的總數）的數量為N，與個別自旋子的可能狀態數（選區的總數）為m。則每個自旋子的狀態函數（每個里可能的所屬選區）為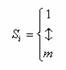 
。而我們的求解目標就是，找出符合給定條件的最低能量組態的自旋子狀態分佈（找出符合給定條件的最好組合的各選區投票所分佈）。
接下來定義各項目標函數。首先是平均人口數條件，我們事先輸入自旋子所受隨機場函數(也就是各里人口數函數) pi。當pi 為定值時，為各里人口數相等。所以某態的總磁化強度（某選區總人口數）Pl，可寫為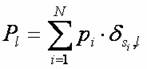
，其中
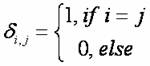，而總人口數為 
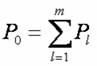，各選區平均人口數為 
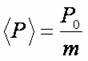。所以我們可以將平均人口數條件寫成以下能量形式：
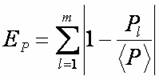。此能量越小時，各選區人口越平均。
再來考慮自旋子最小邊界條件（也就是選區形狀條件）。首先必須定義一個自旋子連接表 Ci,j ，我們定義：鄰近兩自旋子為一，其他為零（兩里相鄰為一，其他為零）
，
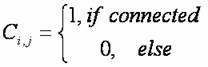，此連接表需事先輸入，已備後用。 然後我們就可寫出最小邊界條件（選區形狀條件）的能量函數。定義自旋子區域(Domain)邊界長度函數，（選區邊界長度函數）為
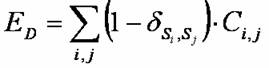，當此函數最小時，各選區位於邊界上的里最少。
另外，我們也考慮其他條件，如希望選區能盡量符合現有行政區域等等。我們使用外場表示現有行政區的影響。定義自旋子外場函數（各里所屬行政區函數）：
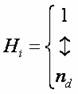，表示每個里所屬行政區（此函數需事先輸入）。則能量函數EA可寫為： 
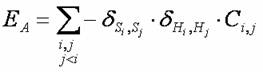。此函數越小，代表每一選區內包含的行政區越少。
最後，我們會得到一個整體目標函數E，如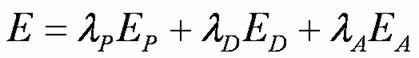 
。調整 l
，以改變各條件的重要性。然後求出不同參數下的解，就可得到不同考慮下的選區劃分的結果。
真實世界資料的轉換：
接下來，我們要做一些準備工作，才能實際計算選區劃分。以下就逐步說明：
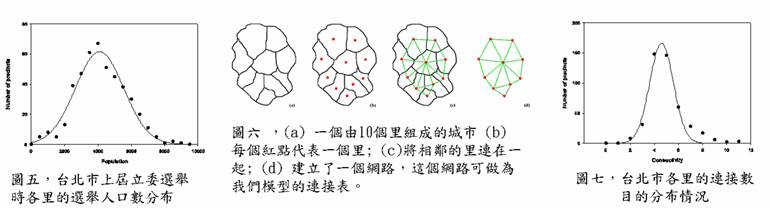
一，資料收集：收集以縣市為運算目標下的選舉資料。包含縣市內的各行政區名稱、各里名稱及各行政區選舉人口、各里選舉人口等等（圖五）顯示台北市上屆立委選舉時各里的人口數分布。另外還要收集地理資料，如精細到里的縣市行政地圖。
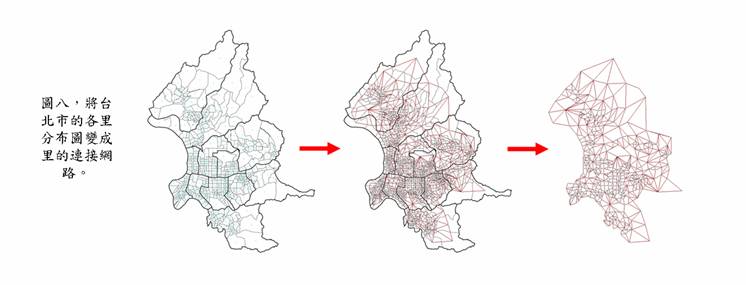
二，資料處理：我們將運算目標縣市內的每個里給予編號，並將選舉人口數及位置建為資料庫。再配合行政區域(里)地圖，將之前各里編號與地圖上里的位置作對應後標示於地圖上，以利連接表製作。我們再觀察地圖上每一個里的相鄰個數數量及編號，由此建立連接表。圖六顯示連接表的製作程序簡圖，圖七顯示連接數目的分布情況。
數值求解：
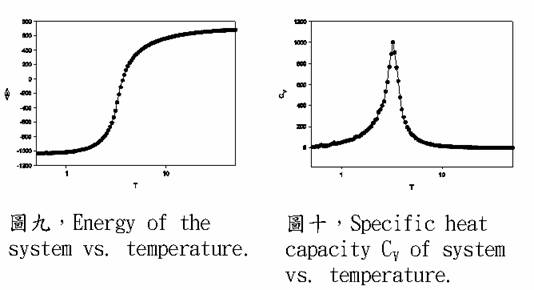
在我們有了目標函數及完成準備工作後，就可利用最佳化方法尋找此複雜系統的基態，也就是求出最符合我們要求條件的解。首先我們利用模擬退火法做了一些測試，也得到了一些結果。而且在利用模擬退火法做測試時，我們看到一些有趣的結果。如圖九顯示溫度與系統平均能量的關係，圖十顯示溫度與系統比熱的關係。顯示了本系統可能存在一些相變現象。
另外，我們也利用遺傳算法來求解此問題，以檢測模擬退火法的結果。由我們目前的結果看來，遺傳算法在這個題目上的搜尋能力較弱，並沒有找到更好的結果。這可能是遺傳算法中的交配及突變型態選擇或參數調控的問題，也可能是這個選區劃分問題本質上的特色。目前我們還在檢驗中。
初步結果：
接下來展示我們的一些初步結果。表一顯示不同參數下的一些計算結果（這裡暫時不考慮行政區域的限制，令
lA 為零）
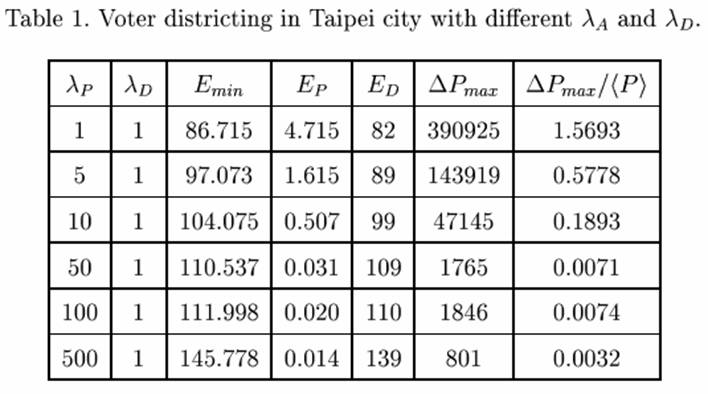
表一中，Emin 代表最低能量，EP 能量代表人口偏差值（越小越好），ED 能量代表選區邊界上里的數量（越小越好），DPmax 代表各選區人口與平均人口數的差值，DPmax/<P> 代表此差值與選區平均人口數的比。
接下來展示我們對台北市做選區劃分的一些結果圖。
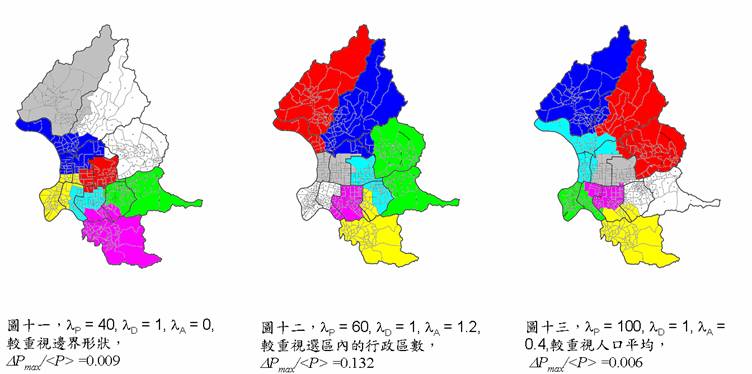
系統的拓展：
由於我們在用模擬退火法做測試時 ，顯示了本系統可能存在一些相變現象。所以我們把系統做了一些拓展。建立了一些不同形式假想城市（圖十四），使它們的人口數及連接關係數也如同真實世界的高斯分佈。然後進行計算，也得到了類似的相變現象。這顯示我們可能可以計算相變的各臨界指數等普適性質（Universality）。
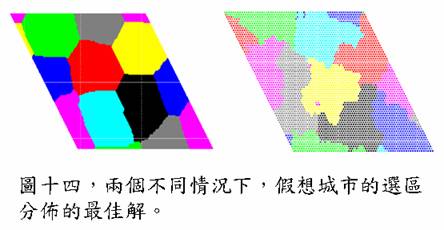
結語：
選區劃分問題是一個難得的，物理學與政治學交叉研究的問題。它的研究結果可以實際運用在現實政治與社會問題上。這裡我們介紹了以台北市為例，如何利用統計物理方法進行選區劃分。並也展現了一些結果。
最後，我們希望將這套分析及計算的方法，應用在更多相關問題上。包含一些社會與物理交叉問題[4,5,6]、組合最佳化問題[7]，及其他形式的區域劃分問題（如學區的劃分，樓層分配（Floor Planning Problem）），以及如“q-partitioning of graph
problem”、“chromatic number problem[8]”與“community detection in network and society[9,10]”等問題上。
參考資料：
[1]
“Taming the Gerrymander--Statistical Physics Approach to Political
Districting Problem”, Chung-I Chou, Sai-Ping Li,
(Submitted), arXiv.org e-Print
archive: physics/0511237。
[2]
薩孟武，1971，《政治學》，台北：三民書局。
[3] R.B. Potts, Proc. Camb. Phil. Soc. 48 (1952) 106.
[4] J.P.Bouchard
and M. Potters, Theory of Financial Risks (
[5] R.M. Mantefna
and H.E. Stanley, An Introduction to Econophysics (
[6] J. Voit,
The Statistical Mechanics of Financial Markets (Springer,
[7] Y. Fu and P.W. Anderson, J. Phys.
A: Math. Gen. 19 (1986) 1605.
[8] P.Y. Lai and Y.Y. Goldschmidt, J.
Stat. Phys. 48 (1987) 513;
[9] M.E.J. Newman, Euro. Phys. J. B38 (2004) 321.
[10] G. Palle et.al.,
Nature 435 (2005) 814.
[11] 另外介紹一個相關的政治與物理交叉研究的網站，臺灣政治期貨交易中心(Taiwan Political Exchange)